你应该具备的基础知识
Vectors向量及其基础运算Dot Product点乘Cross Product叉乘Matrices矩阵
变换是计算机图形学中最基础的部分了,就像加减乘除之于数学。二维和三维图形的平移、旋转、缩放和投影;把一个对象从一个位置、尺寸或方向转换到另一个等等。通过变换,我们可以创建出各种复杂的图形效果:动画、变形和透视等。变换还可以用于相机视图的调整,以及在三维场景中实现物体的移动、旋转和缩放等操作。
二维变换
让我们先从简单的二维变换开始
缩放(以原点为中心)
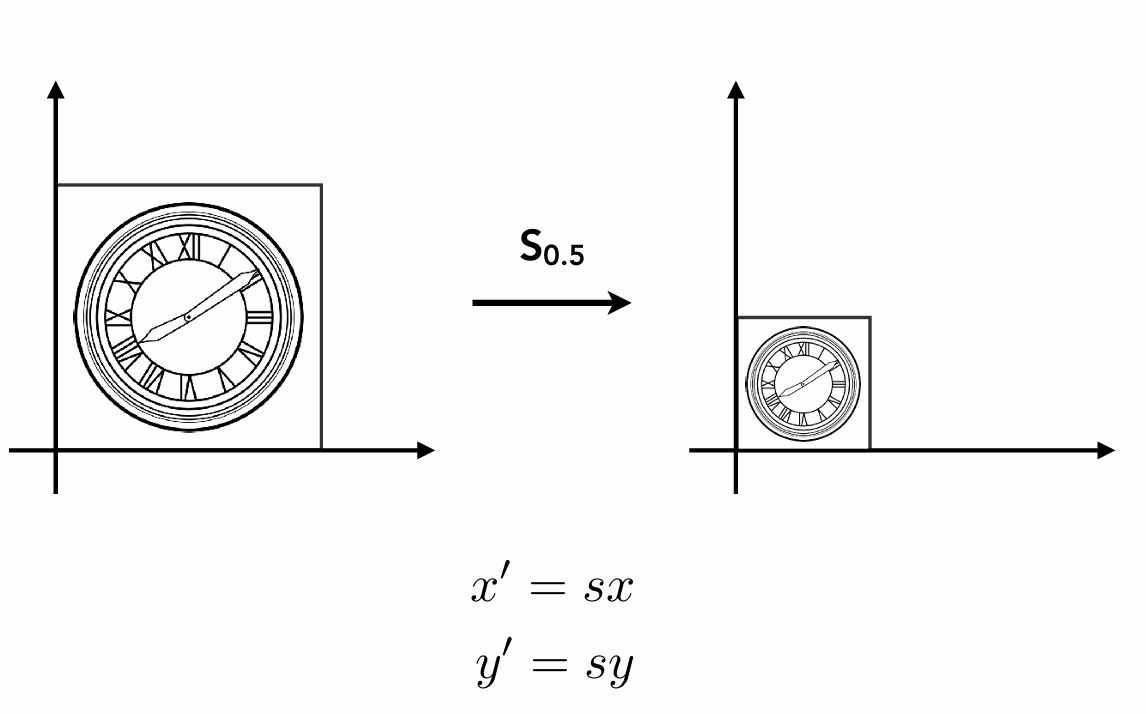
可以用矩阵表示为:
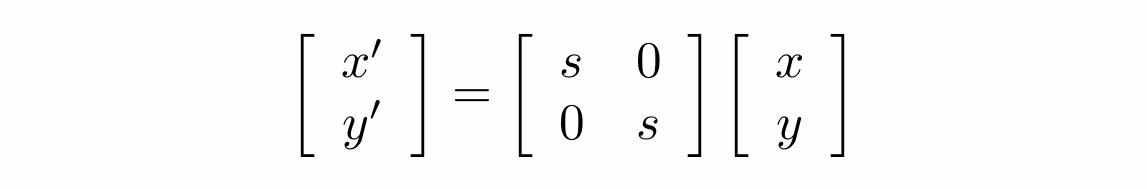
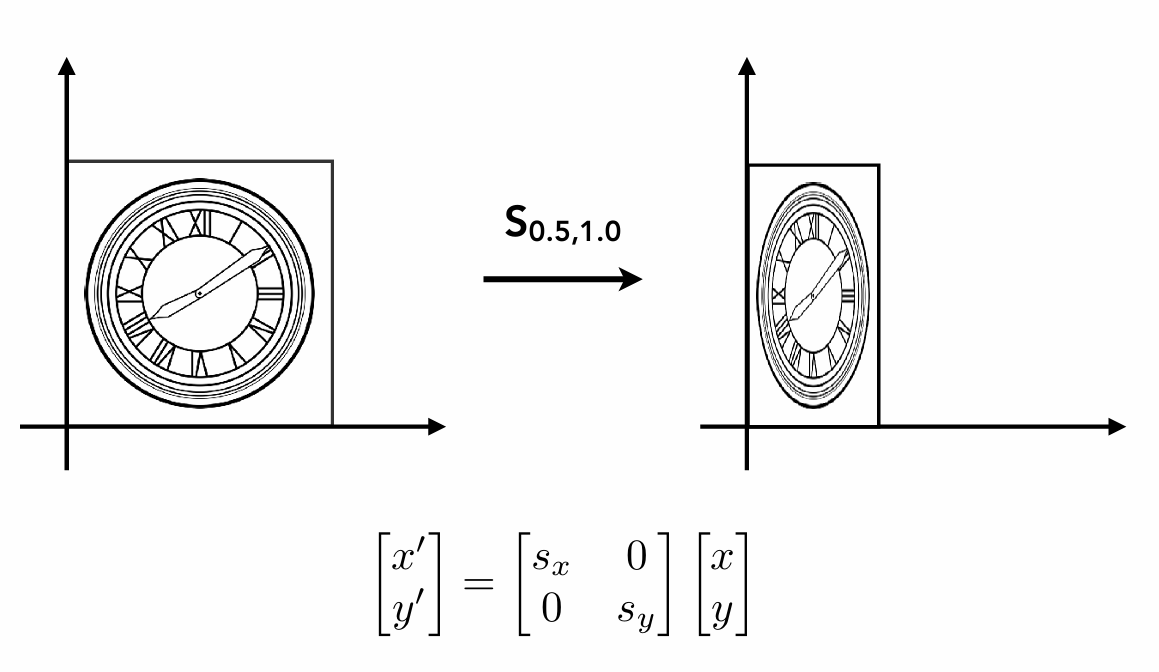
对于不同比例的缩放:
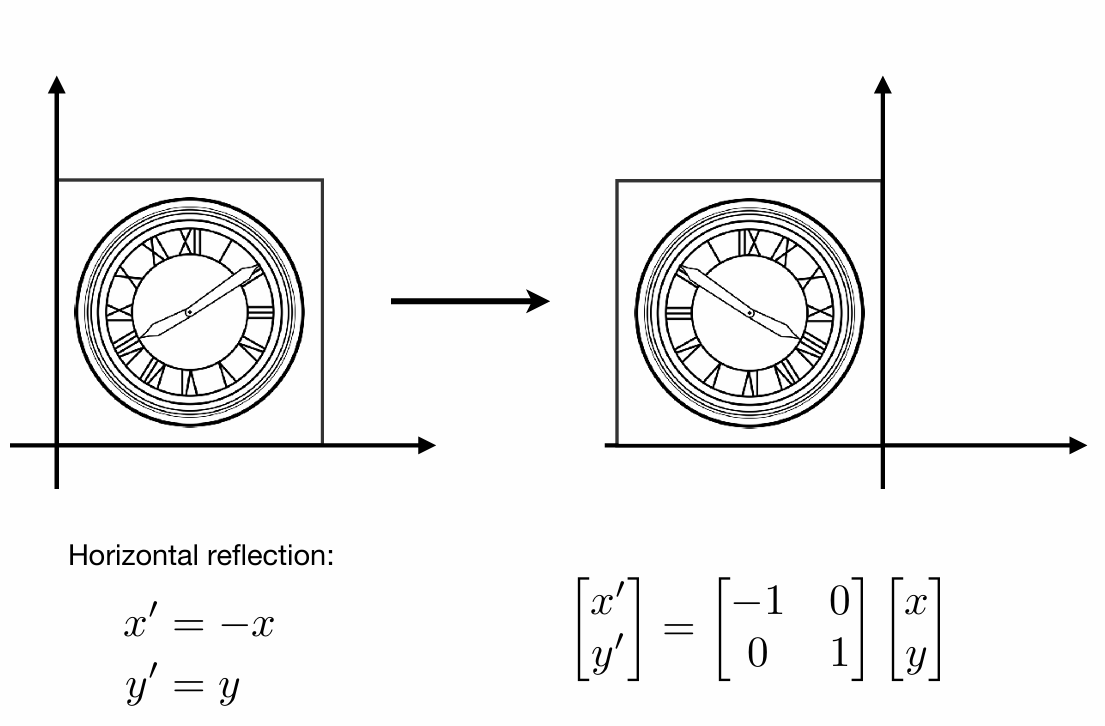
同样的可以推出翻转:
对于这种切变:
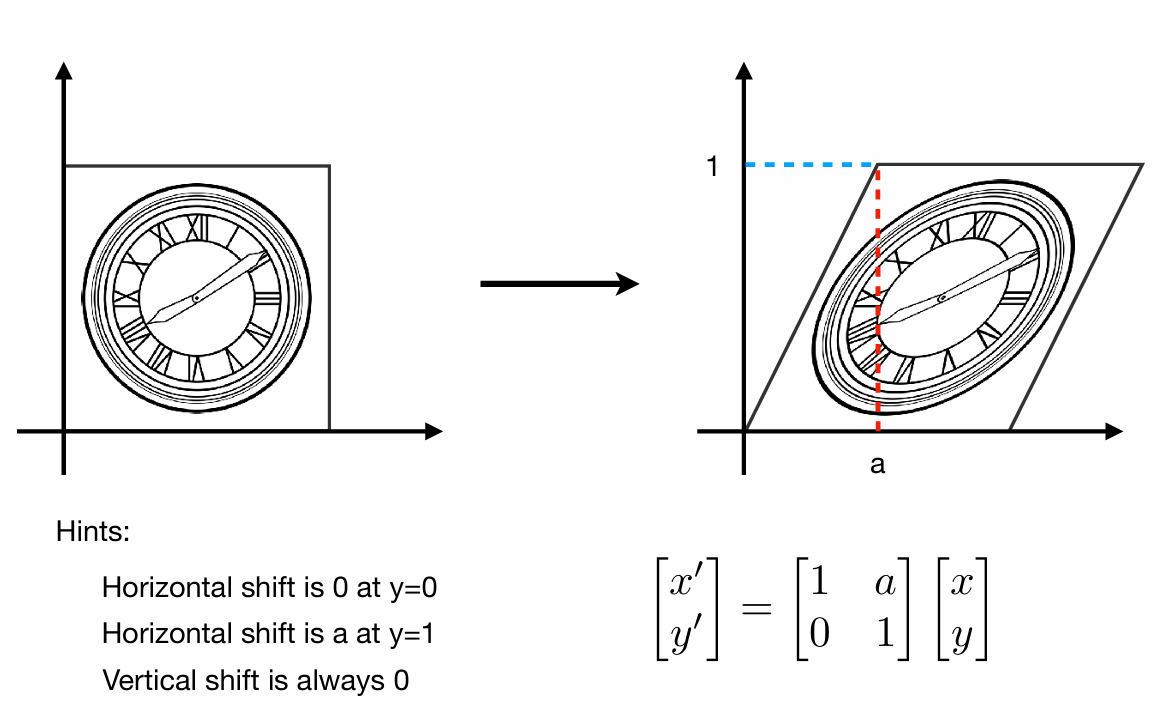
如果我们有一个点P(x, y),应用上面的切变变换后,它的y坐标始终不变,只有x在水平方向上发生变化;而且当y=0时,水平方向上的变化为0,y=1时,水平方向上的变化为a。我们可以取(0,1) -> (a,1)这一点的变换来推出矩阵:
你可以试试其他点,都符合这个规律。
其中矩阵的第一行表示x轴方向上的变换,第二行表示y轴方向上的变换。切变矩阵中的元素s表示在x轴方向上的切变比例。当s为正值时,表示向右上方切变;当s为负值时,表示向左上方切变。
接下来是重头戏:旋转(以原点为中心)
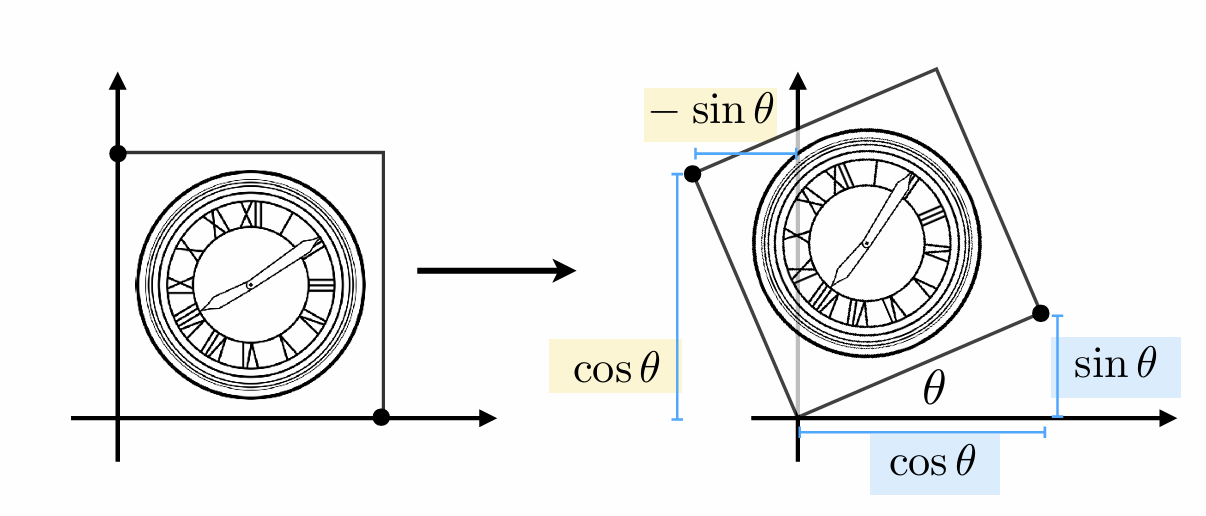
我们还是取特殊点:(1,0)、(0,1)的变化来推导 对于(1,0)点,它在旋转 θ 角后变成了(cosθ,sinθ):
写成矩阵就是:
而对于(0,1)点,它在旋转 θ 角后变成了(-sinθ,cosθ):
写成矩阵就是:
把他们合并起来:
所以旋转矩阵就是:
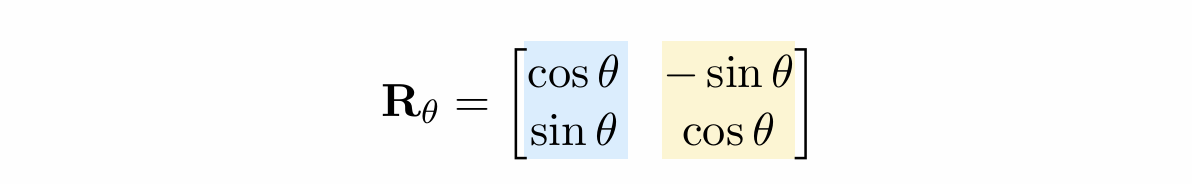
Tips
如果我们想要绕这个点旋转角,按照前面的方法得出的矩阵就是:
可以看到,同时我们知道一个变换的逆变换就是对应矩阵的逆,于是可以得出:
这个矩阵的逆等于它的转置,所以它是一个正交矩阵。
有旋转就有平移:
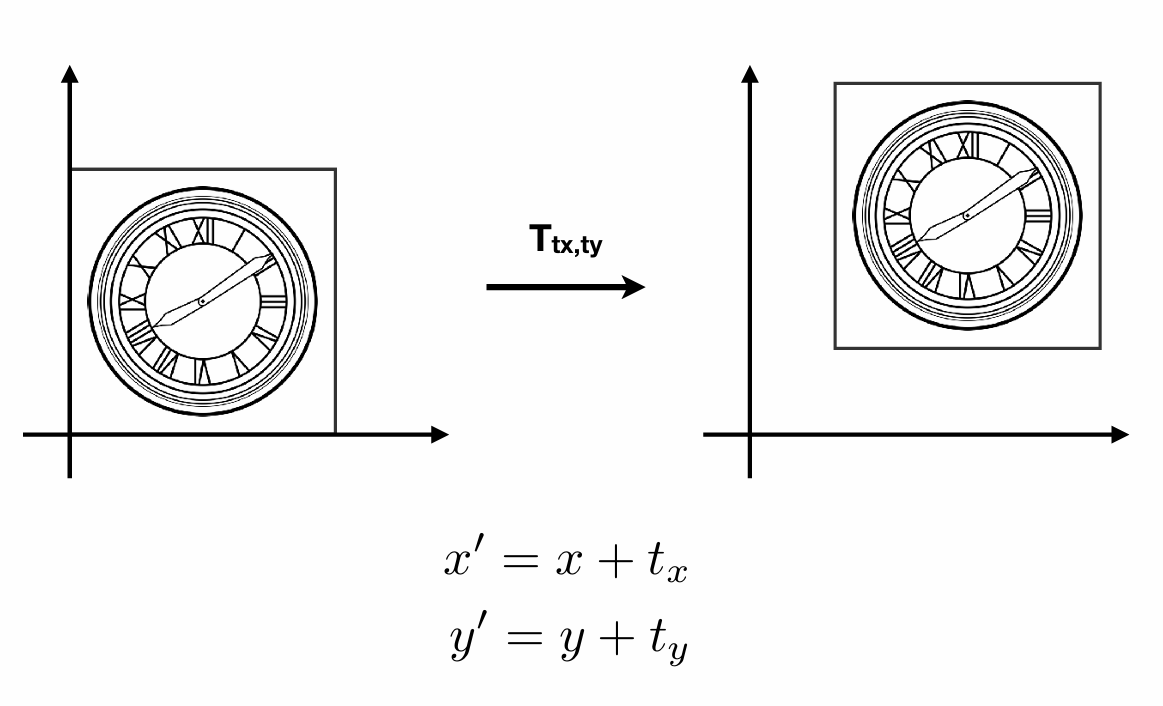
看起来很容易不是吗? 但是如果一个物体既会旋转又要平移,该怎么表示?
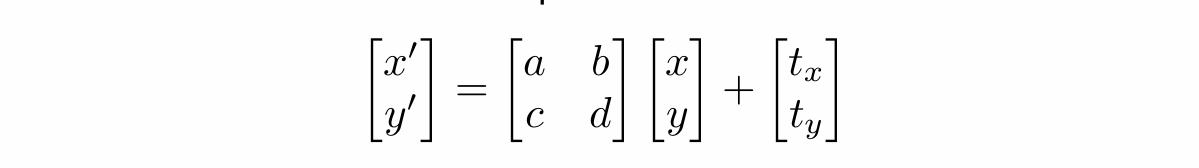
平移变换无法用矩阵相乘的形式表示出来,所以我们不得不采用上面这种方式来表示它。
但是这太不优雅了!而且,我们也不希望平移成为一种特例,这样对计算机和人来说,表示和计算起来都十分麻烦。有没有一种统一的方式,能够让我们来表示所有的转换? 让我们转变思路,进行“升维打击”:
齐次坐标系
齐次坐标系(Homogeneous Coordinates)是一种在计算机图形学和计算机视觉中常用的表示点、向量和变换的方法。通过引入一个额外的维度,我们能够让点和向量可以用更简洁的方式表示,并且能够方便地进行坐标变换。
对二维坐标系来说,一个点通常由其 x、y 表示。但是,在齐次坐标系中,我们增加一个第三维度:
- 对于二维点,我们将其表示为
- 对于二维向量,我们将其表示为
为什么要这样做? 想一想点和向量的运算:
在齐次坐标系下,
说了这么多,这次我们回头再看之前的变换,就可以用一个统一的线性变换表示出来:
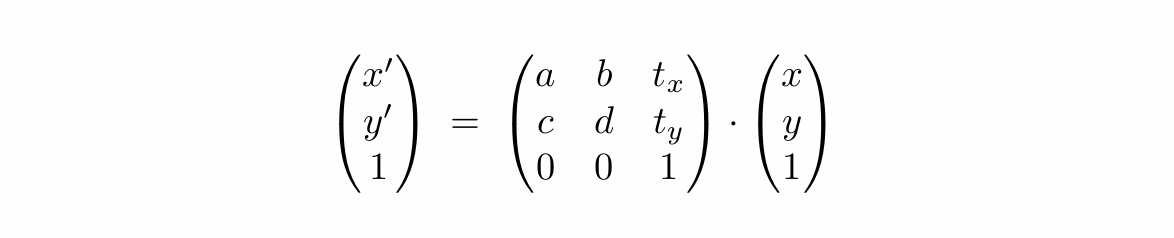
这样二维空间下的坐标变换就可以用一种统一的方式来表示了

Tips
- 矩阵没有交换律:同时需要平移和线性变换的时候,需要先线性变换再平移
- 仿射变换=线性变换+平移
顺序很重要
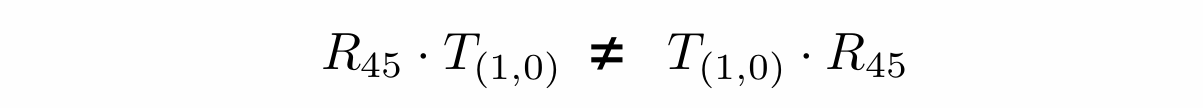
先旋转再平移和先平移再旋转显然是不同的,变换矩阵是从右向左逐个应用的(下图为先旋转再平移):
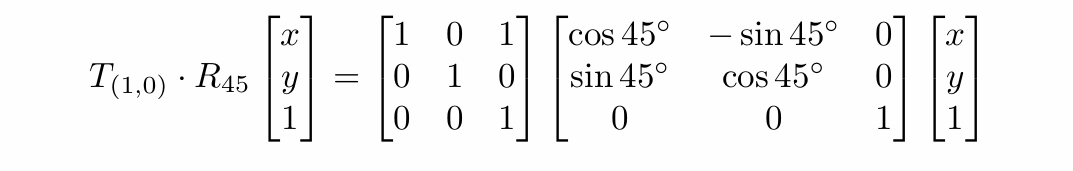
前面我们已经讲过了绕原点旋转,如果我们想绕任一点旋转应该怎么做?
- 将旋转点平移到原点
- 绕原点旋转
- 平移回去
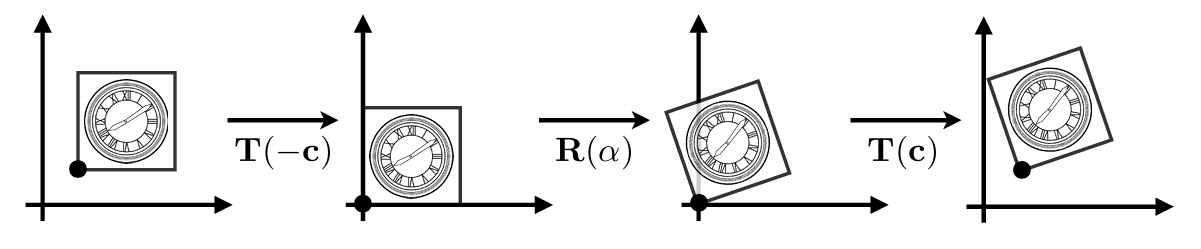
三维变换
表示
与二维同理,只不过多了一个维度:

齐次坐标系也多了一维(像二维变换一样,先线性变换再平移):
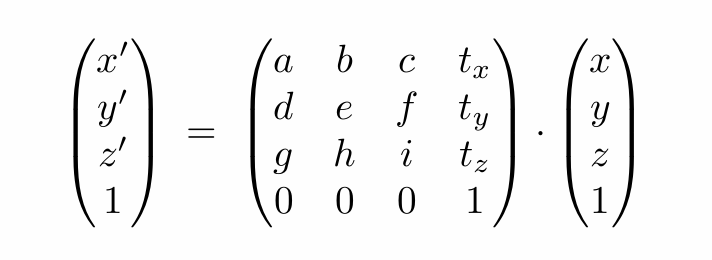
旋转
到了旋转这里,比二维要稍微多一些东西。绕三维空间的某一个轴旋转 角,写成旋转矩阵就像下图:
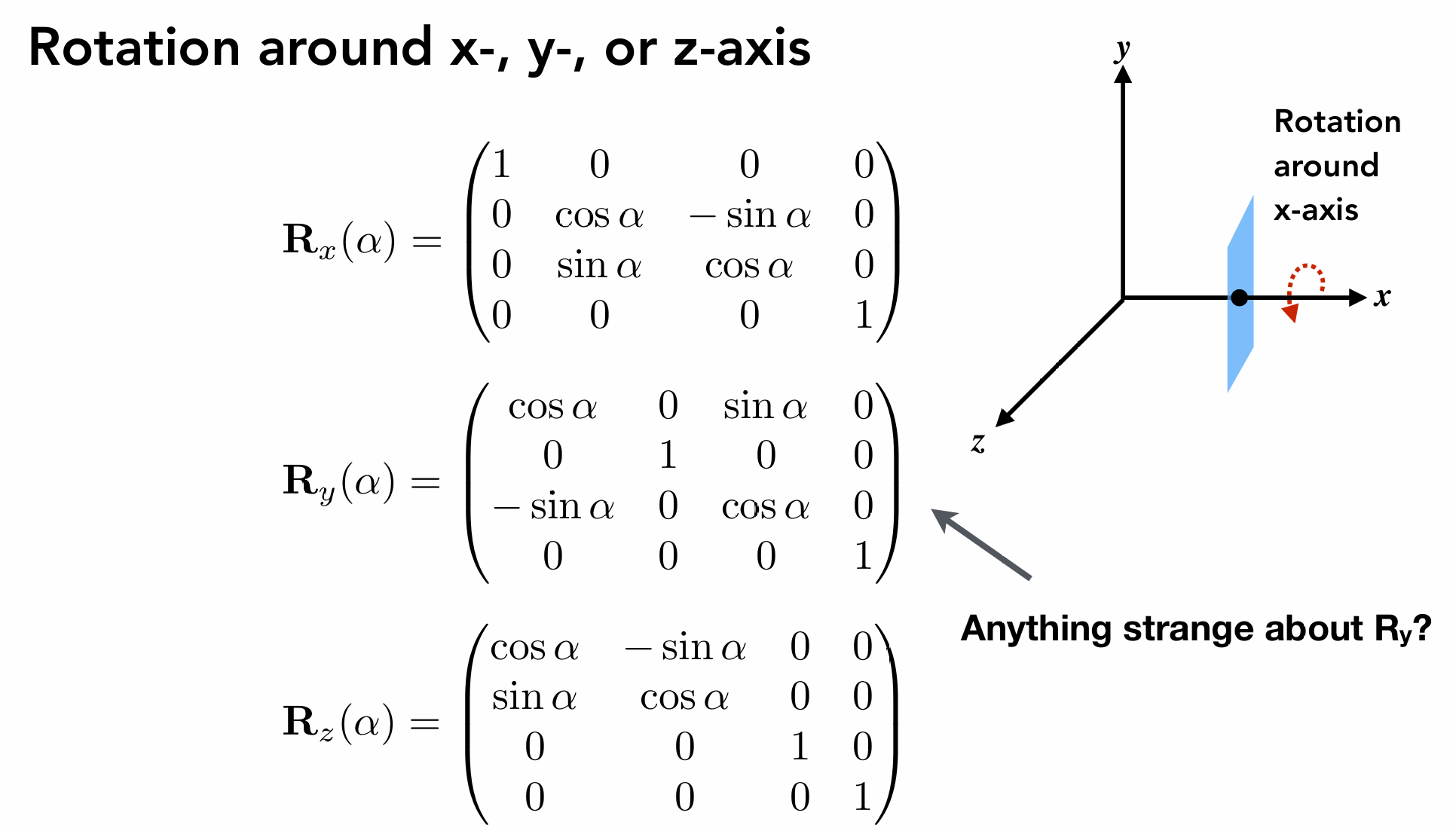
绕 和 轴旋转都很好理解,但是为什么绕 轴旋转成了转置呢?
按照右手螺旋定则绕 x y z 轴进行旋转:
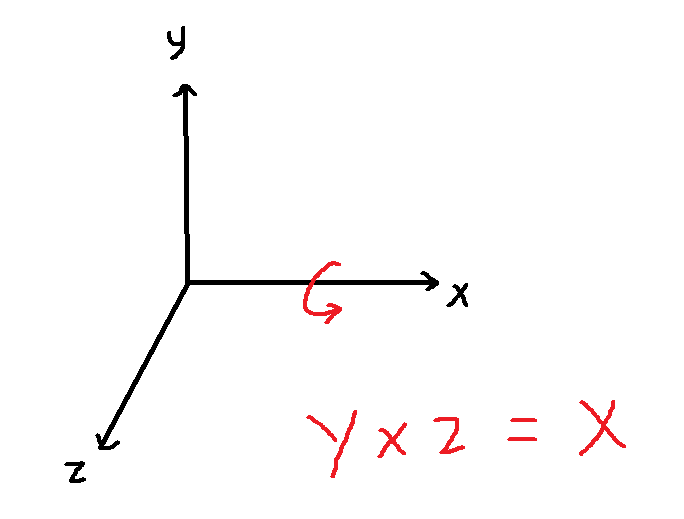
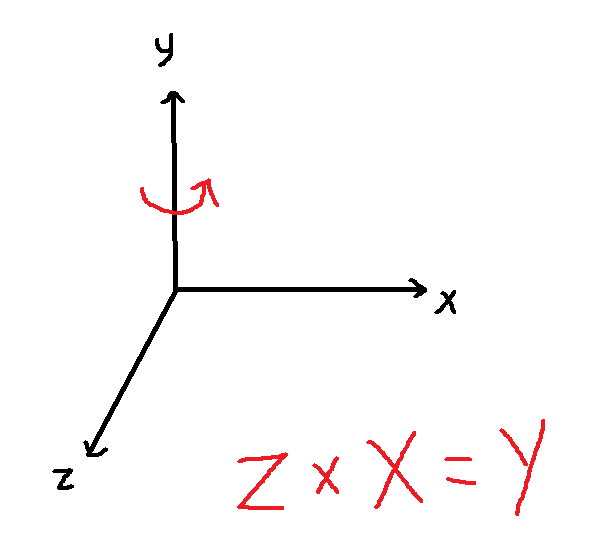
, , 然而 ,所以在 坐标系下旋转是反的,你也可以看作绕y轴的旋转矩阵左上角的3x3矩阵是循环移位后得到的。
欧拉角
我们前面讨论的主要是绕某个固定轴的旋转,那么如果我们想要实现绕任意角度和任意轴的旋转,该如何处理呢?在这种情况下,我们可以引入一种更为灵活的旋转描述方法:欧拉角。欧拉角通过一系列顺序的轴旋转,能够表示任意方向的旋转,为我们提供了一种简单且直观的方式来处理复杂的旋转变换。

在欧拉角的表示中,常见的一种定义方式是使用 Roll(滚转) 、 Pitch(俯仰) 和 Yaw(偏航) 三个角度来描述物体的旋转。这三个角度分别对应于围绕物体自身的三个主要轴的旋转。
视图变换
在前面的部分中,我们讨论了二维和三维空间中的各种几何变换,如平移、旋转、缩放等。这些变换主要用于改变物体在空间中的位置和形状。然而仅仅描述物体的空间位置和形状是不够的。为了将三维场景正确地投影到二维屏幕上,我们还需要引入一种新的变换:视图变换。
什么是视图变换
如果现在我们想拍一张照片,我们至少要做三件事,这对应着视图变换的三个部分:
- 找一个风景不错的地方,让模特摆好姿势(模型变换 Model transformation)
- 找一个好角度并放好相机(视图变化 View transformation)
- 按下快门(投影变换 Projection transformation)
如何定义相机
要做出视图变换之前,我们还得先知道相机的位姿。我们可以用三个量定义相机:
- position(相机在哪)
- look-at direction(朝哪个方向)
- up direction(向上的方向:相机的歪斜程度)
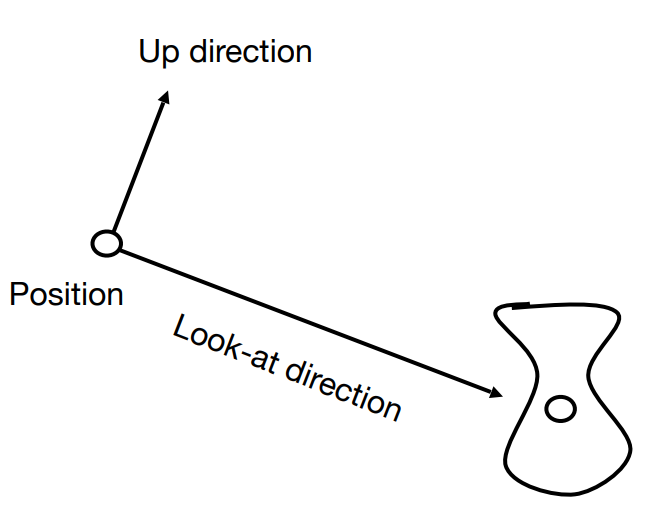
如果相机和物体做相同的运动,那么拍出来的图片肯定是完全一样的:
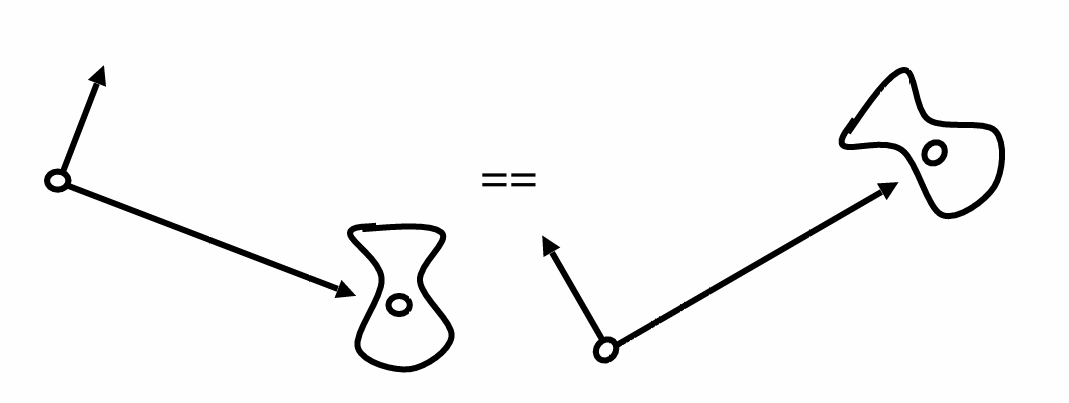
这样的话我们可以将相机放在一个固定位置上,方便后续的变换。
我们把相机原点移动到坐标原点处,令Y为向上方向,让相机视线朝向-Z,并随摄像机变换其他的对象。
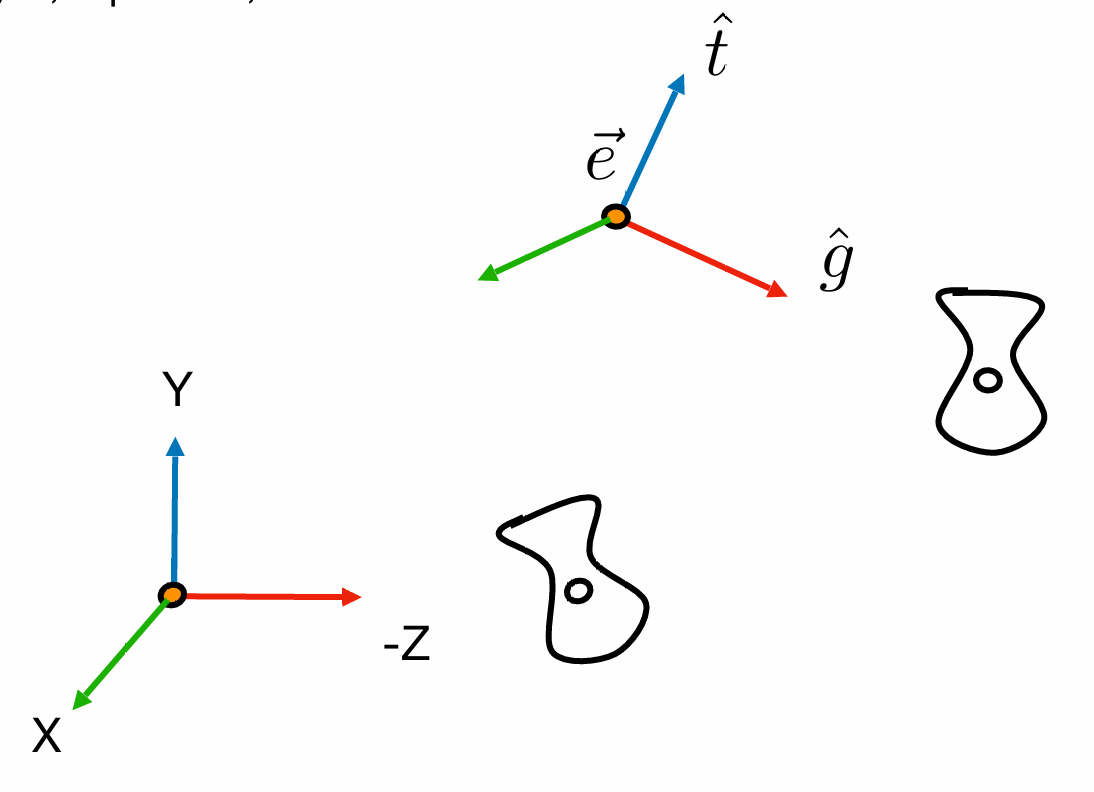
将任意相机移到原点位置
相机的变换矩阵可以写成
我们先将相机平移到坐标原点:
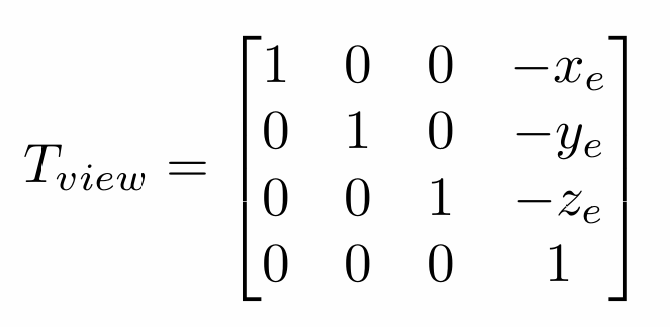
将相机从一个随机的位姿旋转到坐标轴上(向上方向到Y,相机视线朝向-Z)显然是十分困难的;不过,我们可以逆向思维,先求出从原点到相机的旋转矩阵,再求逆就可以得到我们想要的结果:

